An Example

Let's begin applying the process to our original example:

Step 1

First, we move the constant term to the right side by adding 1.5 to each side of the equation:

We may now proceed to Step 2 since all other terms are already on the left side of the equation.

Step 2

The coefficient of the x² term is 1, so we may skip Step 2.

Step 3

We determine that is the coefficient of the x term. Now we divide this coefficient by two , and square it: 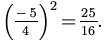. So we now add to each side

Step 4

Now we factor the left side. Even though the left side has fractions, it will always be factorable as x plus half the coefficient of the x term in the original equation (in this case, ).

Step 5

Finally, we take the square root of each side, and make two subproblems.

Subproblem 1:

Subproblem 2:

As we do with factoring, we combine the solutions to the subproblems to determine the solution to the original problem:

Proceed to the next page for a second example.